Do you know this delicious German pastry?

(Photo by Guido Draheim).
It’s called “ Spritzkuchen” or “Spritzring”. I thought of it when I was toying with TikZ and pgfplots. It’s similar to a twisted torus. Today I dealt with it again, when writing on the French TeX question and answer site TeXnique.fr, with the help of my French TeX friends Patrick Bideault and Denis Bitouzé.
Before I come to code and explanation, here are some of the steps and images in the construction process, using pgfplots.
Let’s get a representative cross section. In polar coordinates, the sine function sin(x) gives a circle, sin(3x) are three leaves, we add a bit radius (1.25) as piece in the middle. This gives us the function sin(3x) + 1.25 in polar coordinates:
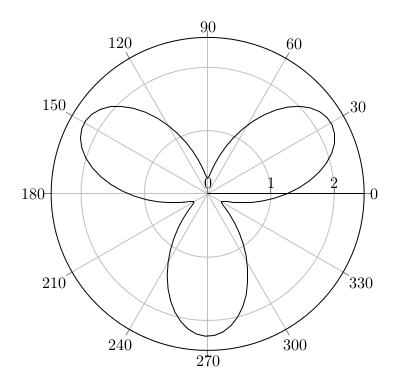
We embed it in the space, such as in the xy plane with z=0 as (x,y,z)(t) = ( cos(t)(sin(3t)+1.25), sin(t)(sin(3t) + 1.25), 0 ):
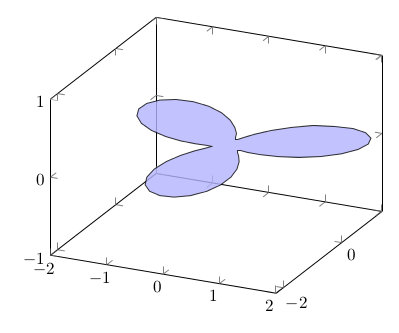
Or differently turned:

We can move it straight through the space for example by drawing in the xz plane and let y run linearly: (x,y,z)(t) = ( cos(t)(sin(3t)+1.25), t, sin(t)(sin(3t)+1.25) ). In space it looks this way:
But we want to turn it. Moving it in a circle in space, we use a torus map, such as:
x(t,s) = (2+cos(t))cos(s+pi/2)
y(t,s) = (2+cos(t))sin(s+pi/2)
z(t,s) = sin(t)
We connect it with our original function:
x(t,s) = (6+(sin(3t)+1.25)cos(t))cos(s)
y(t,s) = (6+(sin(3t)+1.25)cos(t))sin(s)
z(t,s) = (sin(3t)+1.25)sin(t)
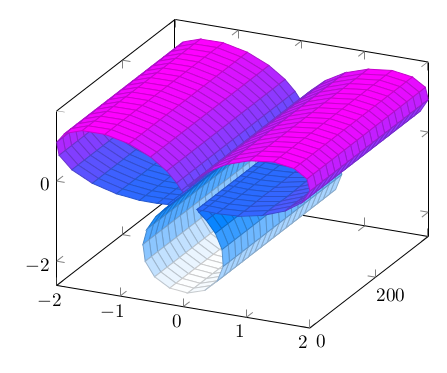
Here is a half section, moved half a turn:

And fully rotated:

And now to the twist. We can twist it by adding a multiple oft t resp. y to the argument of the function. So we achieve a rotation with growing y value:

Not that we did the math and the TeX, let’s frame it:

Ok, code or it didn’t happen.
% Compile with LuaLaTeX because of heavy computations, too hard for pdfLaTeX
\RequirePackage{luatex85}% Only as long as the standalone class is not yet compatible to the newest LuaTeX
\documentclass{standalone}
\usepackage{pgfplots}
\usetikzlibrary{backgrounds}
\begin{document}
\begin{tikzpicture}
\begin{axis}[axis equal,
hide axis,
/tikz/background rectangle/.style = {
left color = black,
right color = black!20,
shading angle = 135,
},
show background rectangle
]
\addplot3[
surf,
shader = flat,
miter limit = 1,
domain = 0:360,
y domain = 0:360,
samples = 100,
samples y = 70,
z buffer = sort,
colormap/hot2,
]
( {(6+(sin(3*(x+3*y))+1.25)*cos(x))*cos(y)},
{(6+(sin(3*(x+3*y))+1.25)*cos(x))*sin(y)},
{((sin(3*(x+3*y))+1.25)*sin(x))} );
\end{axis}
\end{tikzpicture}
\end{document}
All the code and the explanation can be read here – it developed over time:
- German: Drehtransformation mit pgfplots, original post on TeXwelt.de
- English: Rotation transformation of a parametrized plot, with answer by cmhughes on TeX.SE
- French: Représenter un vissage à l’aide de pgfplots, final version on TeXnique.fr
Nice, but I can’t get it to work:
! Package PGF Math Error: Unknown function `em’ (in ‘ {(6+(sin(3(x+3y)
)+1.25)cos(x))cos(y)}’).
I am using TexLive 2017
Hi Jörg,
thanks! The Markdown plugin affected the code example. It makes *text* to emphasized/italic text, according to Markdown syntax, even in a code box, so we got the em HTML tags. That should not happen. I fixed it.
Stefan